Archivos mensuales: octubre 2024

A. A. Kirillov AAKirillov@mephi.ru
B. S. Murygin MuryginBS@gmail.com
Universidad Nacional de Investigación Nuclear MEPhI
(Instituto de Física e Ingeniería de Moscú)

Resumen

Se discute la formación de solitones (objetos estables en física) a través de la dinámica clásica de dos campos escalares en un espacio-tiempo de (2+1) dimensiones. Se muestra que, bajo ciertas condiciones en el Universo temprano, tanto los muros de dominio como las cuerdas cósmicas pueden formarse, incluso si los campos escalares son del tipo inflatón (asociados a la inflación cósmica).

Palabras clave: solitones, cuerdas, paredes de dominio

PACS: 03.50.-z, 11.27.+d, 98.80.Cq

1 Introducción

Los modelos de inflación de múltiples campos, como la inflación híbrida [1] o la inflación natural [2, 3], pueden contener potenciales de formas no triviales. Si el potencial tiene al menos un punto de silla, la dinámica de campo en tales modelos puede conducir a la formación de estructuras topológicamente no triviales llamadas solitones [4-6]. Además, bajo ciertas condiciones, pueden producir agujeros negros primordiales en la era de radiación debido al colapso de paredes de dominio [7] o bucles de cuerdas cósmicas [8] que afectan al universo temprano [9].

Anteriormente, se demostró que los solitones pueden formarse en el espacio-tiempo (1+1) incluso si el potencial tiene solo un mínimo y al menos un punto de silla [10, 11]. En este artículo, continuamos estudiando esta posibilidad en el espacio-tiempo (2+1).

2 Modelo en el espacio-tiempo (2+1)

Consideremos la dinámica de dos campos escalares reales φ y χ con el lagrangiano del sistema

L = 1/2 g^μν (∂_μφ∂_νφ + ∂_μχ∂_νχ) – V(φ, χ), (1)

donde g^μν es el tensor métrico de Friedman-Robertson-Walker con el factor de escala cósmico a(t). Entonces, las ecuaciones de movimiento clásicas para φ y χ en el espacio-tiempo (2+1) toman la forma

φ_tt – 3Hφ_t – φ_xx – φ_yy = -∂V/∂φ,
χ_tt – 3Hχ_t – χ_xx – χ_yy = -∂V/∂χ.
(2)

Aquí, H = ȧ/a es el parámetro de Hubble, que es H_I ~ 10^13 GeV durante la inflación y se vuelve más pequeño en la era de radiación. Para las ecuaciones (2), el parámetro de Hubble juega el papel de un término de fricción, y su dependencia temporal no afecta nuestras conclusiones. Por lo tanto, asumimos que permanece constante después del final de la inflación. Además, el parámetro de Hubble H proporciona una escala natural para todas las unidades. Por lo tanto, expresamos todas las variables dimensionales en unidades de H_I.

Para resolver el sistema (2), debemos definir las condiciones iniciales y de contorno. Elegimos las condiciones iniciales en la forma

φ(x, y, 0) = R cos Θ + φ_1, φ_t(x, y, 0) = 0;
χ(x, y, 0) = R sin Θ + χ_1, χ_t(x, y, 0) = 0,
(3)

donde

R(r) = R_0 cosh^(-1) (r_0/r), Θ = θ. (4)

Esto establece una correspondencia entre el espacio de campos (φ, χ) y el plano físico (x, y). Aquí, el punto (φ_1, χ_1) corresponde al centro del área inicial de campos en forma de disco circular con radio R(r) y ángulo polar 0 ≤ Θ ≤ 2π, r = √(x^2 + y^2) y θ son una distancia desde el origen de coordenadas y un ángulo polar en un plano físico xy, respectivamente, y R_0 y r_0 son parámetros positivos.

Las condiciones de contorno se eligen como

φ_x(±∞, y, t) = 0, φ_y(x, ±∞, t) = 0;
χ_x(±∞, y, t) = 0, χ_y(x, ±∞, t) = 0.
(5)

Estudiamos la evolución clásica de los campos escalares φ y χ con el potencial utilizado en [10, 11]:

V = d(φ^2 + χ^2) + a exp[-b(φ – φ_0)^2 – c(χ – χ_0)^2], (6)

donde a, b, c, d son parámetros positivos. El parámetro a establece la altura de un máximo local, b y c establecen su forma, y d es responsable de la pendiente del potencial. El potencial descrito tiene solo un punto de silla y un mínimo, pero podría modificarse fácilmente para obtener cualquier número de puntos de silla agregando términos como el último.

Adicionalmente, consideramos el conocido potencial «sombrero mexicano inclinado» [3]

V = λ(φ^2 + χ^2 – g^2/2)^2 + Λ^4(1 – φ/√(φ^2 + χ^2)), (7)

donde λ, g, Λ son parámetros positivos. El parámetro g establece la posición de un círculo de mínimos degenerados en el caso del sombrero mexicano sin inclinación, λ establece la altura de un máximo local en el punto (φ_0, χ_0) = (0, 0) y Λ establece la inclinación del potencial. Note que la pendiente del potencial hace que los mínimos no sean degenerados. Sin embargo, la no degeneración no es una condición necesaria para la producción de solitones.

La densidad de energía del sistema está dada por

ρ = 1/2 ∑_i ((∂_iφ)^2 + (∂_iχ)^2) + V(φ, χ), (8)

donde las derivadas parciales se toman sobre las variables {t, x, y}.

3 Resultados

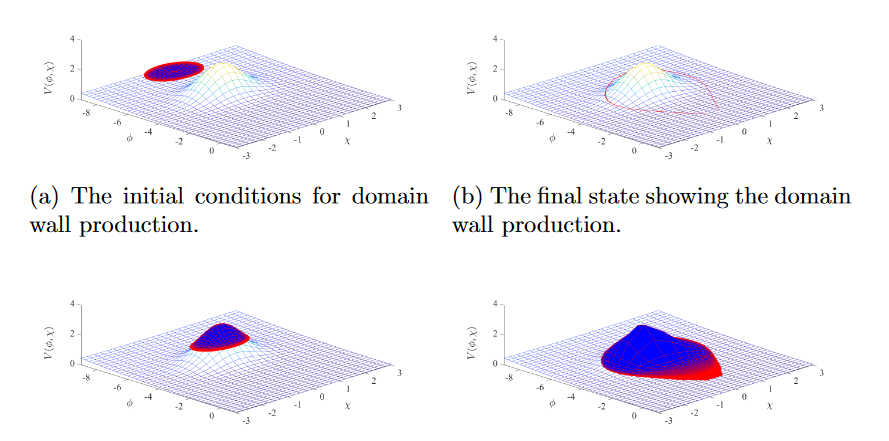
Para el potencial (6), elegimos los parámetros de la siguiente manera: d = 0.005, a = 2, b = 1, c = 1, φ_0 = -5, χ_0 = 0 y los parámetros de las condiciones iniciales (3) R_0 = 1, r_0 = 1, φ_1 = -8 y χ_1 = 0 (todos los valores dimensionales se toman en unidades de H_I). La configuración inicial de los campos está separada del mínimo por el pico del potencial, ver fig. 1a. Note que el potencial tiene el mínimo en el punto (φ_min, χ_min) = (0, 0).

El estado final de la evolución de los campos se presenta en la fig. 1b. Debido a la pendiente del potencial, los campos tienden a alcanzar su mínimo; sin embargo, hay dos formas posibles de lograrlo. Así, los campos pueden rodear el pico por ambos lados. Note que no consideramos la situación en la que la energía del sistema es lo suficientemente grande como para superar el pico sin rodearlo. Como resultado de nuestros cálculos, la configuración alcanza el mínimo de ambas formas posibles y se detiene en el estado de equilibrio.

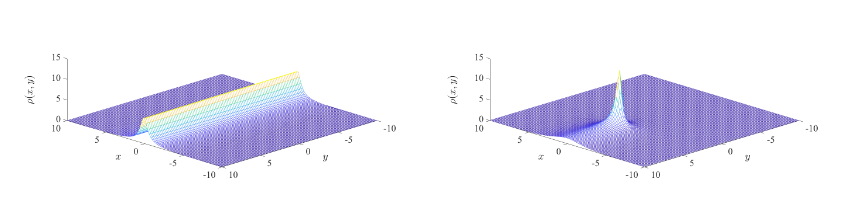
La densidad de energía de la configuración de campos determinada por (8) se presenta en la fig. 2a. Corresponde al tipo bien conocido de solitones llamados paredes de dominio y confirma los resultados de [11] para el número de enrollamiento N = 1. Este solitón estable puede jugar un papel significativo en el universo temprano. Las paredes de dominio cerradas con energía suficientemente alta podrían colapsar debido a la tensión superficial y así producir agujeros negros primordiales [12, 13].

Si fijamos todos los parámetros excepto φ_1, se obtiene el otro tipo de solitones. Elegimos el nuevo valor φ_1 = -5, esto cambia las condiciones iniciales en el espacio de campos (φ, χ), ver fig. 1c. Se puede ver que el estado inicial está ahora en la cima del pico. La evolución del sistema lleva a que los campos tiendan al mínimo del potencial.

Así, la configuración abandona el pico en todas las direcciones. El estado final se muestra en la fig. 1d. La densidad de energía del solitón formado se presenta en la fig. 2b, corresponde a la formación de la cuerda con la cresta. Esto último distingue esencialmente este solitón de las cuerdas bien conocidas.

Es interesante notar que cambiar solo un parámetro φ_1 conduce al otro tipo de solitón. Así, tanto las paredes de dominio como las cuerdas podrían formarse en un mismo modelo. Sin embargo, esto no ocurre para todos los conjuntos posibles de parámetros. La estabilidad de la pared de dominio requiere que el segundo término del potencial (6) correspondiente a la altura del máximo local sea mucho mayor que el primero correspondiente a la pendiente del potencial. Esto impone límites a los parámetros a y d que muestran si se pueden formar paredes de dominio. En el caso de la formación de cuerdas, el parámetro R_0 puede estar restringido porque un valor grande le da al sistema una energía potencial inicial demasiado grande que puede llevar a la destrucción de los solitones.

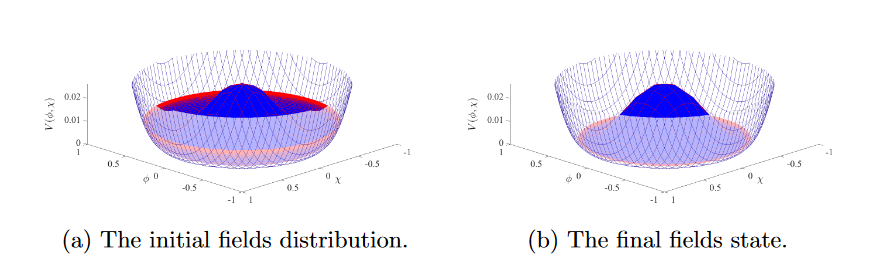
Finalmente, demostremos la formación de solitones en el conocido modelo del sombrero mexicano inclinado (7) que describe la inflación. La posibilidad de producción de paredes de dominio en este potencial se consideró en [11]. Aquí nos enfocamos en el otro tipo de solitones. Elegimos los parámetros del potencial de la siguiente manera: g = 1, λ = 0.1, Λ = 5 · 10^(-13) y los parámetros de las condiciones iniciales R_0 = 0.9, r_0 = 1, φ_1 = χ_1 = 0 (todos en unidades de H_I). Se muestra en la fig. 3a donde el estado inicial de los campos está ubicado en la cima del pico. Debido a que la inclinación es muy pequeña, la configuración de campos se contrae alrededor del pico debido a la tensión superficial y se detiene cuando la pendiente del potencial la compensa (ver fig. 3b).

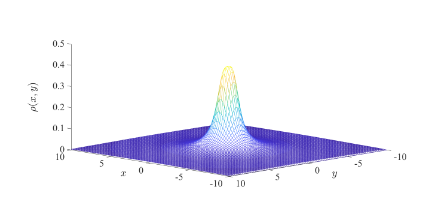
La densidad de energía de la distribución final se presenta en la fig. 4. Se puede ver que corresponde a la formación de una cuerda. La cresta no se ve debido a la pendiente extremadamente pequeña del potencial. Si el parámetro Λ aumenta, aparece la cresta.

4 Conclusión

Se discutió la formación de solitones en el sistema de campos escalares con potenciales que tienen un punto de silla y un mínimo. Se muestra que tanto las paredes de dominio como las cuerdas pueden formarse en el mismo modelo dependiendo de la configuración inicial de los campos. Note que las condiciones iniciales pueden afectar la producción de solitones incluso si los campos escalares son inflatones (esto ocurre si el potencial tiene al menos un punto de silla). En este caso, es importante verificar si aparecen solitones en el modelo para evitar su sobreproducción en el universo temprano y, en consecuencia, agujeros negros primordiales que pueden contradecir los datos observacionales [14].

Agradecimiento

Los autores agradecen a K. M. Belotsky, V. A. Gani y S. G. Rubin por las útiles discusiones. El trabajo fue apoyado por la subvención RFBR No 19-02-00930.

Referencias

• [1] A. Linde, «Hybrid inflation», Phys. Rev. D 49, 748–754 (1994), arXiv:astro-ph/9307002 [astro-ph].
• [2] J. E. Kim, H. P. Nilles, and M. Peloso, «Completing natural inflation», J. Cosmol. Astropart. Phys. 2005, 005 (2005), arXiv:hep-ph/0409138 [astro-ph].
• [3] M. Peloso and C. Unal, «Trajectories with suppressed tensor-to-scalar ratio in Aligned Natural Inflation», J. Cosmol. Astropart. Phys. 2015, 040 (2015), arXiv:1504.02784 [astro-ph.CO].
• [4] R. Rajaraman, Solitons and instantons (North-Holland Publishing Company, Amsterdam, 1989).
• [5] A. Vilenkin and E. Shellard, Cosmic strings and other topological defects (Cambridge University Press, Cambridge, 2000).
• [6] N. Manton and P. Sutcliffe, Topological solitons (Cambridge University Press, Cambridge, 2004).
• [7] K. M. Belotsky et al., «Clusters of Primordial Black Holes», Eur. Phys. J. C 79, 246, 246 (2019), arXiv:1807.06590 [astro-ph.CO].
• [8] T. Helfer, J. C. Aurrekoetxea, and E. A. Lim, «Cosmic string loop collapse in full general relativity», Phys. Rev. D 99, 104028 (2019), arXiv:1808.06678 [gr-qc].
• [9] A. Vilenkin, Y. Levin, and A. Gruzinov, «Cosmic strings and primordial black holes», J. Cosmol. Astropart. Phys. 2018, 008 (2018), arXiv:1808.00670 [astro-ph.CO].
• [10] V. A. Gani, A. A. Kirillov, and S. G. Rubin, «Transitions between topologically non-trivial configurations», J. Phys. Conf. Ser. 934, 012046 (2017), arXiv:1711.07700 [hep-th].
• [11] V. A. Gani, A. A. Kirillov, and S. G. Rubin, “Classical transitions with the topological number changing in the early Universe”, J. Cos-mol. Astropart. Phys. 2018, 042 (2018), arXiv:1704.03688 [hep-th].
• [12] S. G. Rubin, A. S. Sakharov, and M. Y. Khlopov, “The Formation of Primary Galactic Nuclei during Phase Transitions in the Early Universe”, J. Exp. Theor. Phys. 92, 921–929 (2001), arXiv:hep-ph/ 0106187 [hep-ph].
• [13] M. Y. Khlopov, S. G. Rubin, and A. S. Sakharov, “Primordial struc-ture of massive black hole clusters”, Astropart. Phys. 23, 265–277 (2005), arXiv: astro-ph/0401532 [astro-ph].
• [14] B. Carr et al., “Constraints on Primordial Black Holes”, arXiv: 2002. 12778 [astro-ph.CO].